[Programmers-Java] 산 모양 타일링

https://school.programmers.co.kr/learn/courses/30/lessons/258705

접근

n = 1일 때
n = 2일 때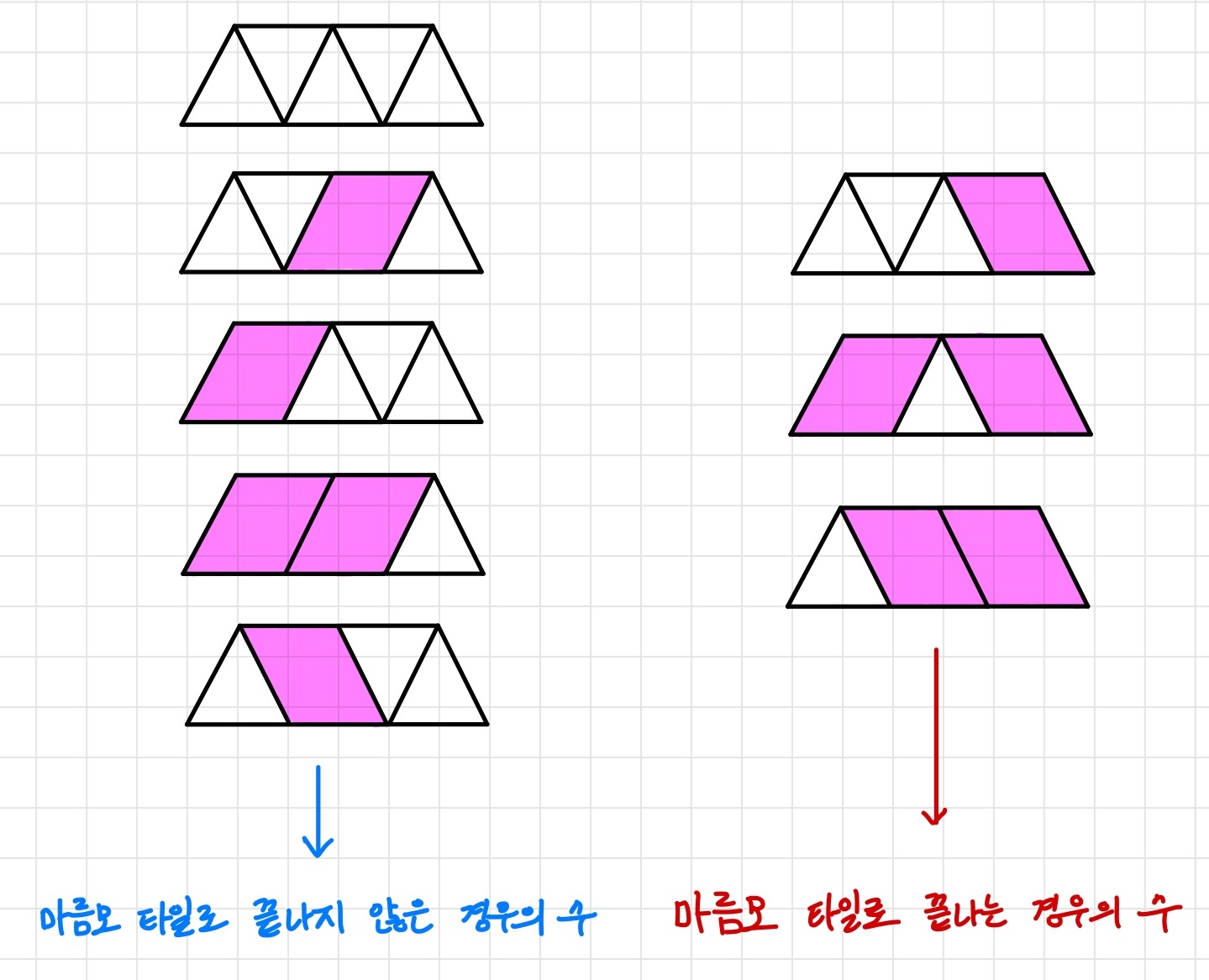
마름모 타일로 끝나지 않은 경우의 수는
마름모 타일로 끝나는 경우의 수는 n - 1번째의 모든 경우의 수에서 오른쪽으로 마름모 타일을 붙이면 된다.
마름모 타일로 끝나지 않은 경우의 수를 dp[n][0], 마름모 타일로 끝나는 경우의 수를 dp[n][1]이라고 할 때
dp[n][0] = dp[n - 1][0] * 2 + dp[n - 1][1]
dp[n][1] = dp[n - 1][0] + dp[n - 1][1]
n번째에 tops가 있으면 dp[n][0] = dp[n - 1][0] * 3 + dp[n - 1][1] * 2가 된다.

풀이

class Solution {
    public int solution(int n, int[] tops) {
        int mod = 10007;
        int[][] dp = new int[n][2];
        dp[0][0] = tops[0] == 1 ? 3 : 2; // (1)
        dp[0][1] = 1;
        for (int i = 1; i < n; i++) {
            int mul1 = tops[i] == 1 ? 3 : 2;
            int mul2 = tops[i] == 1 ? 2 : 1;
            dp[i][0] = (dp[i - 1][0] * mul1 + dp[i - 1][1] * mul2) % mod;
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
        }
        return (dp[n - 1][0] + dp[n - 1][1]) % mod;
    }
}